The four possible data scenarios
This serves as a quick guide to four possible scenarios that relate to whether the likelihood function has a true global maximum. A detailed exposition on the issues
discussed here may be found on our
'understanding fitting' page or in
Prins
(2019). Note that fitting fails described here aren't exactly
fitting fails, rather they are
data fails (scenarios -1, -2, and -3 occur when there is no maximum in the likelihood
function that can be found). If your likelihood function contains a global maximum and you use an appropriate search grid (type 'help PAL_PFML_Fit'), Palamedes will find that global maximum.
The 4 different scenarios:
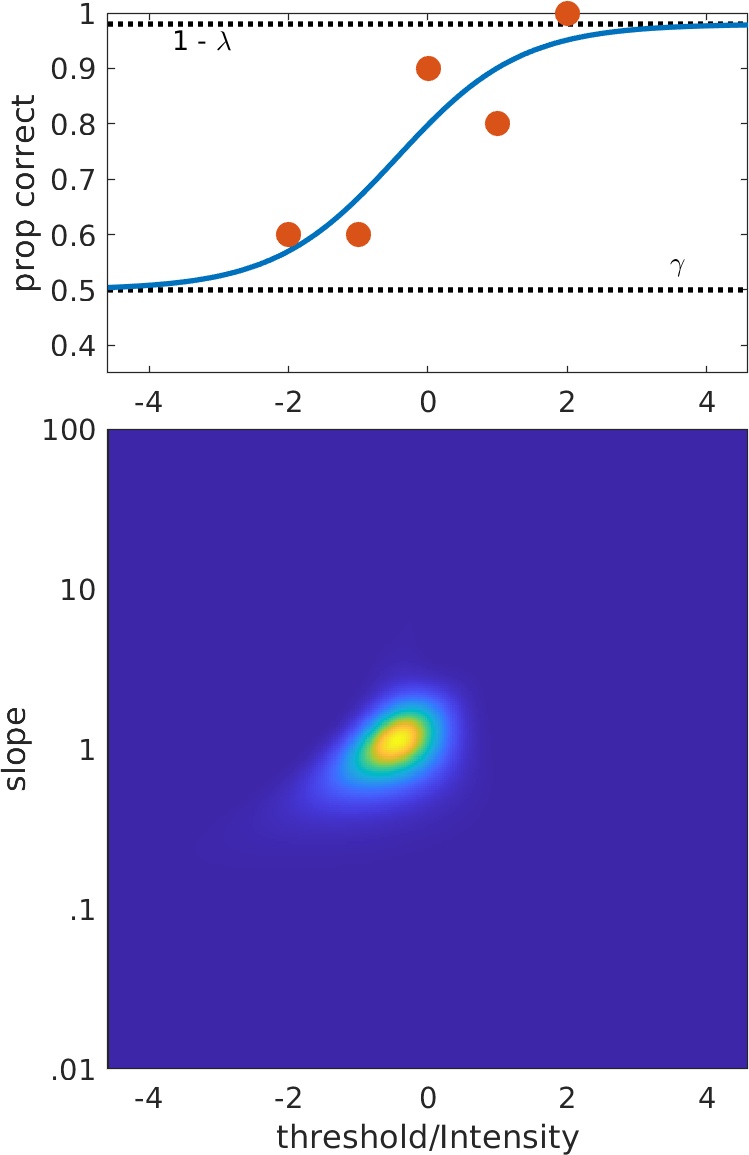
Scenario 1:
Scenario 1: all is well, your likelihood function has a global maximum.
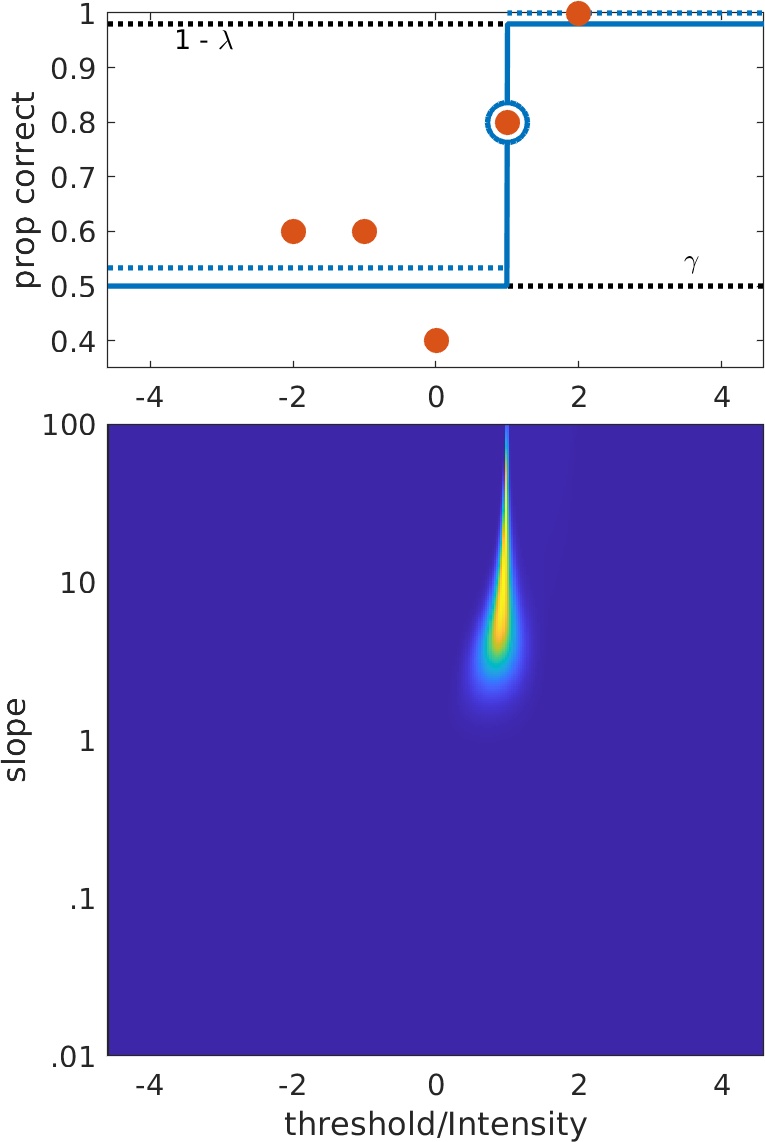
Scenario -1:
Scenario -1: Step function with one intermediate point fits better than any sigmoid (but can be approached asymptotically by a sigmoid).
Solid blue line is best-fitting step function
with guess and lapse rate fixed. Broken lines show best-fitting with guess and/or lapse rate freed.
Problem: Stimulus placement is too wide and/or too few observations (trials) were made.
Even though the fit technically failed (because data are deficient, mind you: It's you, not us) information is still there: Location ('threshold') parameter is likely near location of step.
Slope parameter is likely very high (relative to spacing of placement anyway).
Solutions:
Redo experiment with narrower stimulus placement (consider adaptive placement).
Add observations.
Fix slope at reasonable value.
Go Bayesian: PAL_PFHB_modelFit.
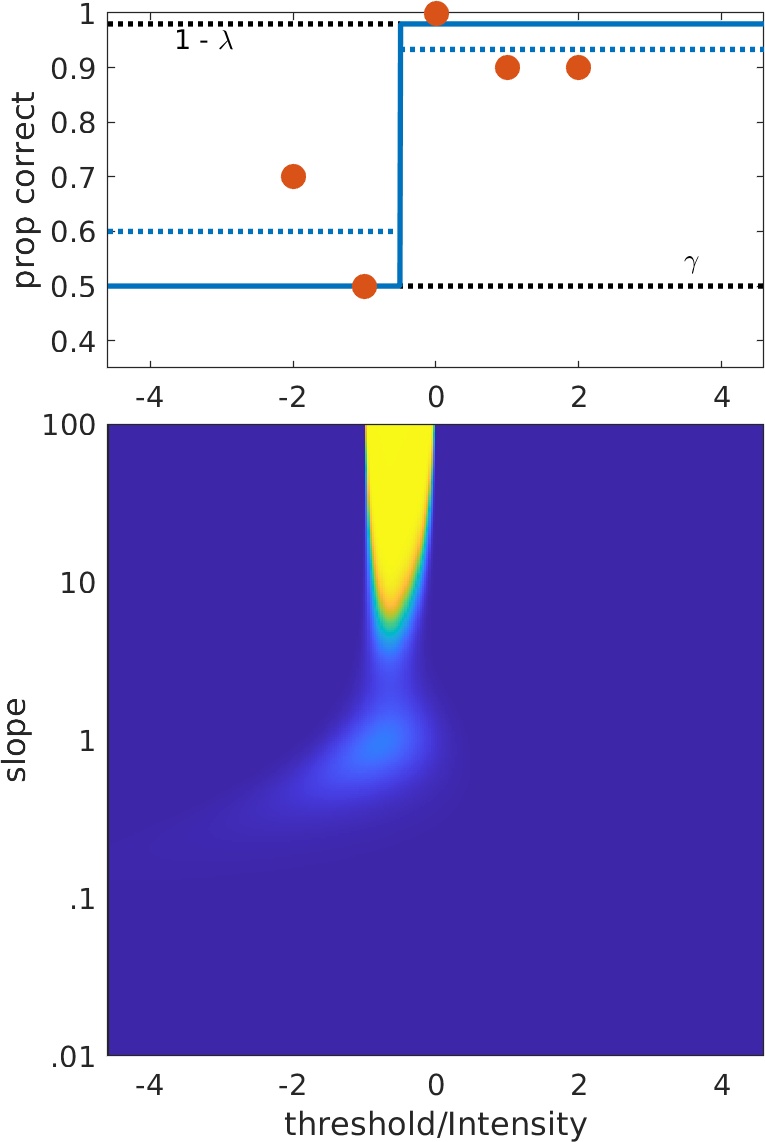
Scenario -2:
Scenario -2: Similar to scenario -1 but without intemediate point. Solid blue line is best-fitting step function with guess and lapse rate fixed. Broken lines show best-fitting with guess
and/or lapse rate freed.
Problem: Stimulus placement is too wide and/or too few observations (trials) were made. Even though the fit technically failed (because data are deficient, mind you:
It's you, not us) information is still there: Location ('threshold') parameter is likely near location of step. Slope parameter is likely very high (relative to spacing of placement anyway).
Solutions:
Redo experiment with narrower stimulus placement (consider adaptive placement).
Add observations.
Fix slope at reasonable value.
Go Bayesian:
PAL_PFHB_modelFit.
Scenario -3:
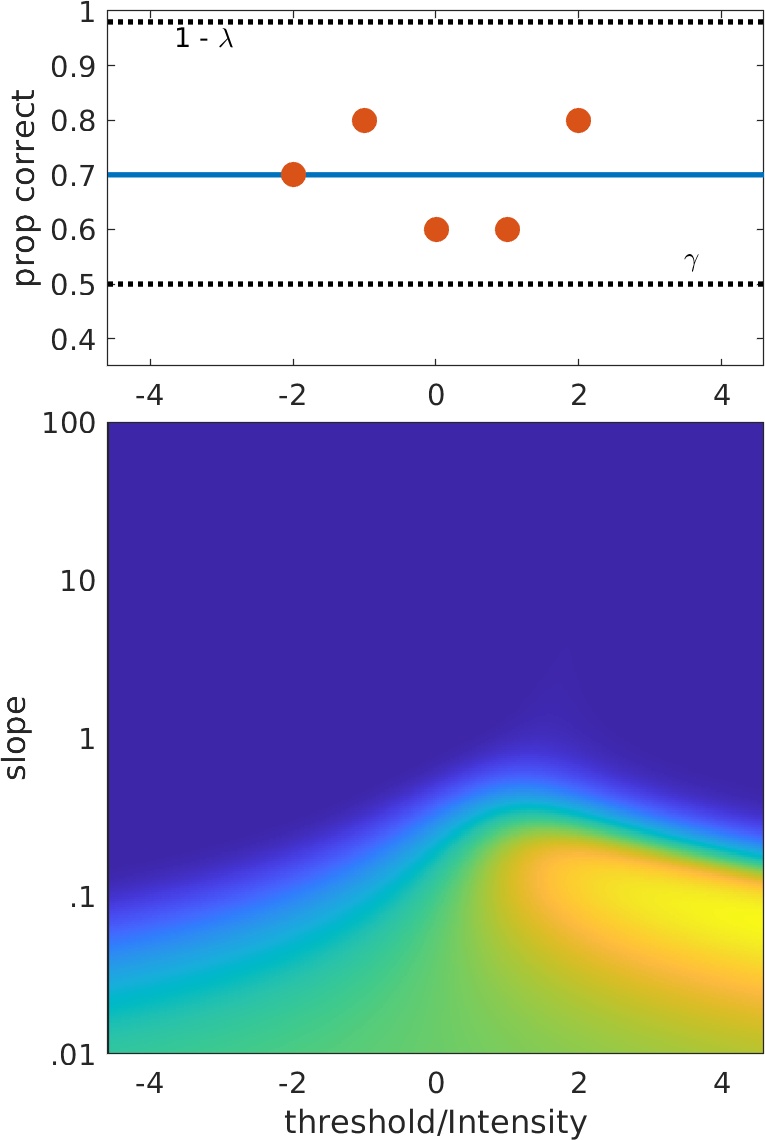
Scenario -3: Constant function valued at the mean proportion correct across all trials fits better than any increasing sigmoid (but can be approached asymptotically by a sigmoid). Solid blue
line is best-fitting constant function. Any constant function valued between
γ and 1 -
λ (not just at the proportion correct corresponding to the PF's value at threshold!) can be approached
asymptotically by a sigmoid.
Problem: Stimulus placement is too narrow and/or too few observations (trials) were made. Scenario -3 may result when using adaptive method that aims to
place
stimuli near location ('threshold') parameter (e.g., up/down, best Pest, Quest). Very little information here as to what value of location parameter may be but slope parameter is likely low
(relative to the spacing of stimulus placements anyway).
Solutions:
Redo experiment with broader stimulus placement (consider adaptive placement strategy that targets slope as
well as location, e.g., psi-method).
Add observations.
Fix slope at reasonable value.
Go Bayesian: PAL_PFHB_modelFit.
Give it a shot?
Think you can identify the different scenarios by eye? Many, if not most, researchers are very confident they can. Below are 10 data
sets that were generated by a synthetic observer (logistic with location = 0, slope = 1, guess rate = 0.5, lapse rate = 0.02). All 4 scenarios above are represented. Take a stab at them.
The best-fitting function for each will be revealed when you click the image! We've kept it easy: There are only five data points, both the guess and lapse rates are fixed, and all stimulus
intensities are used equally often (10 trials at each intensity). Things would be more difficult if the guess and/or lapse rate are free parameters, more stimulus intensities are used, and
when some intensities are used more than others (e.g., when adaptive method is used).
Can't get enough?
We have an unlimited supply of these in our PAL_PFML_FailedMLFits_Demo in the PalamedesDemos folder! Also available with free lapse rate.