Hello,
I have been using PAL_PFHB_fitModel to fit psychometric functions through my data using Palamedes 1_10_7. I've got two conditions with multiple participants each (same participants for both condtions). I set both the guess rate and the lapse rate as "unconstrained". I noticed that the individual lapse estimates never go down to 0, even for those participants for whom other models (for instance Maximum Likelihood with guess and lapse unconstrained) would produce a lapse estimate of 0. I wondered whether the default prior for the lapse rate in the Bayesian Hierarchical Model in Palamedes is somehow set to be >0. If so, is it possible to change it with multiple conditions and participants? I tried, for example, to change the prior distribution for 'l' from Beta to Unif, using [0,1] as third parameter, but that somehow crashed the program.
Thank you in advance,
Aurelio
Lapse Rate
- Nick Prins
- Site Admin
- Posts: 28
- Joined: Sun Feb 13, 2022 8:55 pm
Re: Lapse Rate
Glad to hear that you’re using PAL_PFHB and got it to work. Awesome. More people should do so. To answer your question: When you analyze data from multiple observer simultaneously using PAL_PFHB_fitModel, it will perform a hierarchical analysis. That is, besides modeling the individual lapse rates, it will also model the distribution of lapse rates across the observers. This will have the effect that the estimate of any observer’s lapse rate will be influenced by the estimates of all the other observer’s lapse rates. So, if you have ten observers and nine of them show evidence of lapsing but the tenth does not, the model ‘believes’ that your tenth observer lapse rate also is not zero. Note here that ‘not showing evidence of lapsing’ (say getting all ten of ten trials placed at a very high intensity stimulus correct) is still consistent with having a lapse rate (i.e., the true underlying probability of producing a lapse on any given trial, not the proportion of trials that one actually lapsed) greater than zero, while showing evidence of lapsing (say missing one of ten very high intensity trials) is not consistent with having a lapse rate equal to zero. Thus, the data for the observer that correctly responded to all ten very high intensity trials contains little information as to what the lapse rate for that observer may be (data are consistent with lapse rate = 0 as well as lapse rate > 0). The hierarchical model’s estimate is based on: 1. the data (very little information there), 2. the prior (deliberately set to something not very ‘informative’ to keep the frequentists from yelling at us) and 3. what may be learned from other observers about what lapse rates are like. 1. and 2. contain very little information regarding the lapse rate and so the model’s best guess is that this observer’s lapse rate is like the lapse rate of the other observers (but somewhat lower than the lapse rate estimate of the observers who did miss some of those ten very-high-intensity trials).
Note also that Bayesian estimates aren’t really point values (rather they are distributions). Priors also. So Palamedes doesn’t ‘set’ the lapse rate to a particular value but rather to a distribution of values. The default prior for the lapse rate has it’s mode at 0, by the way. You should download Palamedes 1.10.10 or greater, run your analysis, then run this command: PAL_PFHB_drawViolins(pfhb, ‘l’) [replace 'pfhb' with whatever you named your structure]. It will produce an image like that shown below which shows the posteriors for the lapse rates as violin plots. The observer/condition who according to ML fit was estimated to have lapse rate = 0 likely shows significant density at a value of 0. The results shown here resulted from running PAL_PFHB_MultipleSubjectsAndCoditions_Demo but with lapse rates 'unconstrained'.
When you set prior for lapse rate values to 'uniform' things crash indeed because of the hierarchical model. The default priors for the lapse rate hyperparameters aren’t appropriate when using uniform priors for individual-level uniform priors. You can fix this but you'd end up with a worse model. And you still wouldn't get a lapse rate estimate of 0 (and you shouldn't, because of the above).
Rant alert! I would consider using ‘constrained’ for lapse rate (and possibly guess rate, depends on what the guess rate actually measures) unless you have a very good reason not to. I can not stress this enough (I really can not, trust me, I tried): Typically, individual data sets (one observer, one condition) contain virtually no information as to what the lapse rate may be. Let me try to convince you (and maybe others who might read this) to constrain your lapse rate using an example scenario. Here goes. You run an observer through, say, 5 conditions. Let’s say that in each condition you use 100 trials that are governed by Kontsevich & Tyler’s psi-method. That’s great, but those 100 trials will contain virtually no information on the lapse rate. You read somewhere that you should be worried about the lapse rate and estimate it (or ‘free it’, or ‘allow it to vary’, or whatever you want to call it) because that will fix it, so you've read. But you read somewhere else that you shouldn’t free the lapse rate just because you can and instead should only do so if your data actually contain some information about the lapse rate. So you randomly mix 20 ‘free’ trials (i.e., very high intensity trials, observer should get these correct if not for lapsing) in with the 100 psi-method trials. You now have more justification for estimating the lapse rate than most published research does, I would say. Now, let’s say that in condition 1, the observer did get all 20 free trials correct, in condition 2: 18, in 3: 19, in 4: 18, in 5: 17. Given this information, what would be a reasonable guess for what the probability was that the observer lapsed on any of the 100 psi-method trials (i.e., the ones that are informative on what the threshold and slope were) in condition 1? (Note that that is what you really want to know, that is what those 20 free trials are there for, nobody cares on how many of the 20 free trials the observer actually did lapse per se). Before you guess, note that the most likely number correct for the 20 free trials for an observer with any lapse rate of up to about 0.048 is 20 (again: ‘no evidence of lapsing’ and ‘evidence that there is no lapsing’ are two very different things). Here is my guess: Unless you have some reason to believe that the true, underlying probability that the observer lapses on any trial depends on the condition, the most reasonable data-based guess for the lapse rate in condition 1 is 0.08: There were a total of 100 trials the observer should have gotten correct if not for lapsing and the observer missed 8 of them. Note that there is about a 19% chance that an observer with a lapse rate of 0.08 gets all 20 free trials correct. Low and behold: The observer did 5 conditions and in 20% of those conditions the observer did get all 20 free trials correct. Pretty much exactly what you would expect from somebody who has a lapse rate of 0.08. My best guess for the lapse rate in condition 1: 0.08. That’s what you would get if you use ‘constrained’. The insane guess ‘0’ is what you would get with ‘unconstrained’ (at least with ML estimation, with Bayesian estimation it depends on your prior and with hierarchical Bayesian it further depends on what your other observers did, but the issue is the same).
Might as well keep going now. If your guess rate measures lapsing (i.e., the observed proportion of making a particular response for perfect non-lapsing observer in your task would go from 0 to 1, but that of a real, lapsing responder might never make it quite to 0 because of lapses) the same reasoning as above applies. Unless you have reason to believe that the lapse rate at one end is different than it is at the other end (again, talking about the true underlying probability of a lapse, not the actual proportion of trials the observer actually happens to lapse on) you should use the ‘gammaEQlambda’ argument to estimate the single assumed underlying probability of making a lapse.
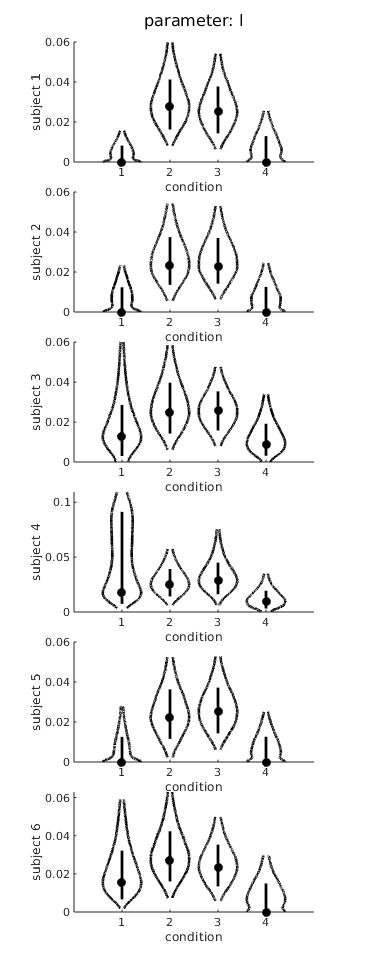
Note also that Bayesian estimates aren’t really point values (rather they are distributions). Priors also. So Palamedes doesn’t ‘set’ the lapse rate to a particular value but rather to a distribution of values. The default prior for the lapse rate has it’s mode at 0, by the way. You should download Palamedes 1.10.10 or greater, run your analysis, then run this command: PAL_PFHB_drawViolins(pfhb, ‘l’) [replace 'pfhb' with whatever you named your structure]. It will produce an image like that shown below which shows the posteriors for the lapse rates as violin plots. The observer/condition who according to ML fit was estimated to have lapse rate = 0 likely shows significant density at a value of 0. The results shown here resulted from running PAL_PFHB_MultipleSubjectsAndCoditions_Demo but with lapse rates 'unconstrained'.
When you set prior for lapse rate values to 'uniform' things crash indeed because of the hierarchical model. The default priors for the lapse rate hyperparameters aren’t appropriate when using uniform priors for individual-level uniform priors. You can fix this but you'd end up with a worse model. And you still wouldn't get a lapse rate estimate of 0 (and you shouldn't, because of the above).
Rant alert! I would consider using ‘constrained’ for lapse rate (and possibly guess rate, depends on what the guess rate actually measures) unless you have a very good reason not to. I can not stress this enough (I really can not, trust me, I tried): Typically, individual data sets (one observer, one condition) contain virtually no information as to what the lapse rate may be. Let me try to convince you (and maybe others who might read this) to constrain your lapse rate using an example scenario. Here goes. You run an observer through, say, 5 conditions. Let’s say that in each condition you use 100 trials that are governed by Kontsevich & Tyler’s psi-method. That’s great, but those 100 trials will contain virtually no information on the lapse rate. You read somewhere that you should be worried about the lapse rate and estimate it (or ‘free it’, or ‘allow it to vary’, or whatever you want to call it) because that will fix it, so you've read. But you read somewhere else that you shouldn’t free the lapse rate just because you can and instead should only do so if your data actually contain some information about the lapse rate. So you randomly mix 20 ‘free’ trials (i.e., very high intensity trials, observer should get these correct if not for lapsing) in with the 100 psi-method trials. You now have more justification for estimating the lapse rate than most published research does, I would say. Now, let’s say that in condition 1, the observer did get all 20 free trials correct, in condition 2: 18, in 3: 19, in 4: 18, in 5: 17. Given this information, what would be a reasonable guess for what the probability was that the observer lapsed on any of the 100 psi-method trials (i.e., the ones that are informative on what the threshold and slope were) in condition 1? (Note that that is what you really want to know, that is what those 20 free trials are there for, nobody cares on how many of the 20 free trials the observer actually did lapse per se). Before you guess, note that the most likely number correct for the 20 free trials for an observer with any lapse rate of up to about 0.048 is 20 (again: ‘no evidence of lapsing’ and ‘evidence that there is no lapsing’ are two very different things). Here is my guess: Unless you have some reason to believe that the true, underlying probability that the observer lapses on any trial depends on the condition, the most reasonable data-based guess for the lapse rate in condition 1 is 0.08: There were a total of 100 trials the observer should have gotten correct if not for lapsing and the observer missed 8 of them. Note that there is about a 19% chance that an observer with a lapse rate of 0.08 gets all 20 free trials correct. Low and behold: The observer did 5 conditions and in 20% of those conditions the observer did get all 20 free trials correct. Pretty much exactly what you would expect from somebody who has a lapse rate of 0.08. My best guess for the lapse rate in condition 1: 0.08. That’s what you would get if you use ‘constrained’. The insane guess ‘0’ is what you would get with ‘unconstrained’ (at least with ML estimation, with Bayesian estimation it depends on your prior and with hierarchical Bayesian it further depends on what your other observers did, but the issue is the same).
Might as well keep going now. If your guess rate measures lapsing (i.e., the observed proportion of making a particular response for perfect non-lapsing observer in your task would go from 0 to 1, but that of a real, lapsing responder might never make it quite to 0 because of lapses) the same reasoning as above applies. Unless you have reason to believe that the lapse rate at one end is different than it is at the other end (again, talking about the true underlying probability of a lapse, not the actual proportion of trials the observer actually happens to lapse on) you should use the ‘gammaEQlambda’ argument to estimate the single assumed underlying probability of making a lapse.

Nick Prins, Administrator