Hello,
I did an experiment on two groups of people, testing hearing sensitivity at two frequencies using the method of constant stimuli. I fitted slope and threshold, fixed lapse at a small, constant value and fix the false alarm rate to the value obtained for the no sound (-Inf) condition in the session. I used a staircase test for getting priors for threshold and the literature for priors of the slope. The fits look good, and the Bayesian fitting has as one of its advantages that it avoids infinity slopes and provides reasonable estimates for the error in the fit parameters.
Now, I would like to test within each group whether slope is different between the two frequencies. I would also like to test whether the two groups differed significantly with respect to slope at either frequency. Fixing the lapse rate to the same value in all fits is straightforward, but is it possible to fix the false alarm rate to the actual value observed per session? Passing a vector after ‘g’, ‘fixed’ to PAL_PFHB_fitModel results in an error.
Similarly, is it possible to set the mean of the threshold prior to different values for different frequencies/subjects?
Gerard
Fixing false alarm rate per condition/subject
- Nick Prins
- Site Admin
- Posts: 28
- Joined: Sun Feb 13, 2022 8:55 pm
Re: Fixing false alarm rate per condition/subject
Hi Gerard,
Glad to hear you find Palamedes useful and gives you good fits.
Currently, the PFHB routines do not allow comparing groups of observers. You can compare individual observers against other individual observers but that’s it. You can of course run two separate analyses, one for each group, then compare posteriors or summary statistics for the hyperparameters (or observer-level parameters) between the two groups.
Palamedes does not directly allow fixing guess rates at different values for different subjects and/or sessions. But there is a work-around to accomplish that. I’ll explain the work-around below. However, before I do that I’m going to try to talk you out of taking that approach. Here goes. Trials at intensities other than ‘-Inf’ contain information on the false alarm rate also. Consider this hypothetical, but not implausible, scenario: Let’s say an observer responds ‘yes’ on a proportion of 0.4 of foil (‘-Inf’) trials. Let’s also say that on the trials where the lowest intensity (but greater than -Inf) is used, the observer responds ‘yes’ on a proportion of, say, 0.3 of trials. The latter of course would suggest that 0.4 might be an overestimate of the false alarm rate. What should you use for the probability of the false alarm rate? Is it better to fix it at .4 or to let the model do its thing and take into account all the information? Note that you can include the ‘-Inf’ trials in the overall analysis (just use the value ‘-Inf’ as an intensity value, I demonstrate this in the code below). If the data at the trials where intensity was not ‘-Inf’ give little information about the value of the false alarm rate, then you’ll find that Palamedes’ estimate for the guess rate appropriately will be close to the observed proportion ‘yes’ at ‘-Inf’ trials (assuming the prior is not too informative). But if there is information at the other trials (as in the above hypothetical example), the model will, again appropriately, adjust its estimate accordingly. Another way to think about it is that using a fixed value for a parameter in a Bayesian analysis is equivalent to supplying an infinitely narrow prior (or point prior). In other words, you would be pretending that there is no uncertainty regarding the value of the false alarm rate. But there is uncertainty, and so you would be misinforming the model. And if you misinform your model, your results suffer.
Here is the workaround for fixing the false alarms rate at different values for different conditions. Code given is for a single observer analysis. The strategy is to specify different priors in the different conditions and make those priors very tight. In the example code, the gues rate for condition 1 would (effectively) be fixed at 0.1, for condition 2 at .2. You can generalize to a multiple observer analysis. You would have to create a very tight prior on gmu parameter at the to-be-fixed value and create a prior on gkappa that only contains very high values. That would force all guess rates to be near the targeted value. Again, we recommend against all of this.
Yes, you can use different means (or sds if you like) for priors in different conditions (see demo code below).
In order to test whether slope parameters differ between conditions, the recommended strategy is to reparameterize the two slopes into a mean (across conditions) slope parameter and a difference-between-slopes parameter. The test criterion could then be to determine whether 0 is a credible value for the difference parameter.
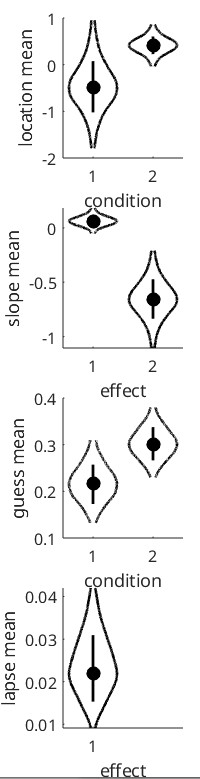
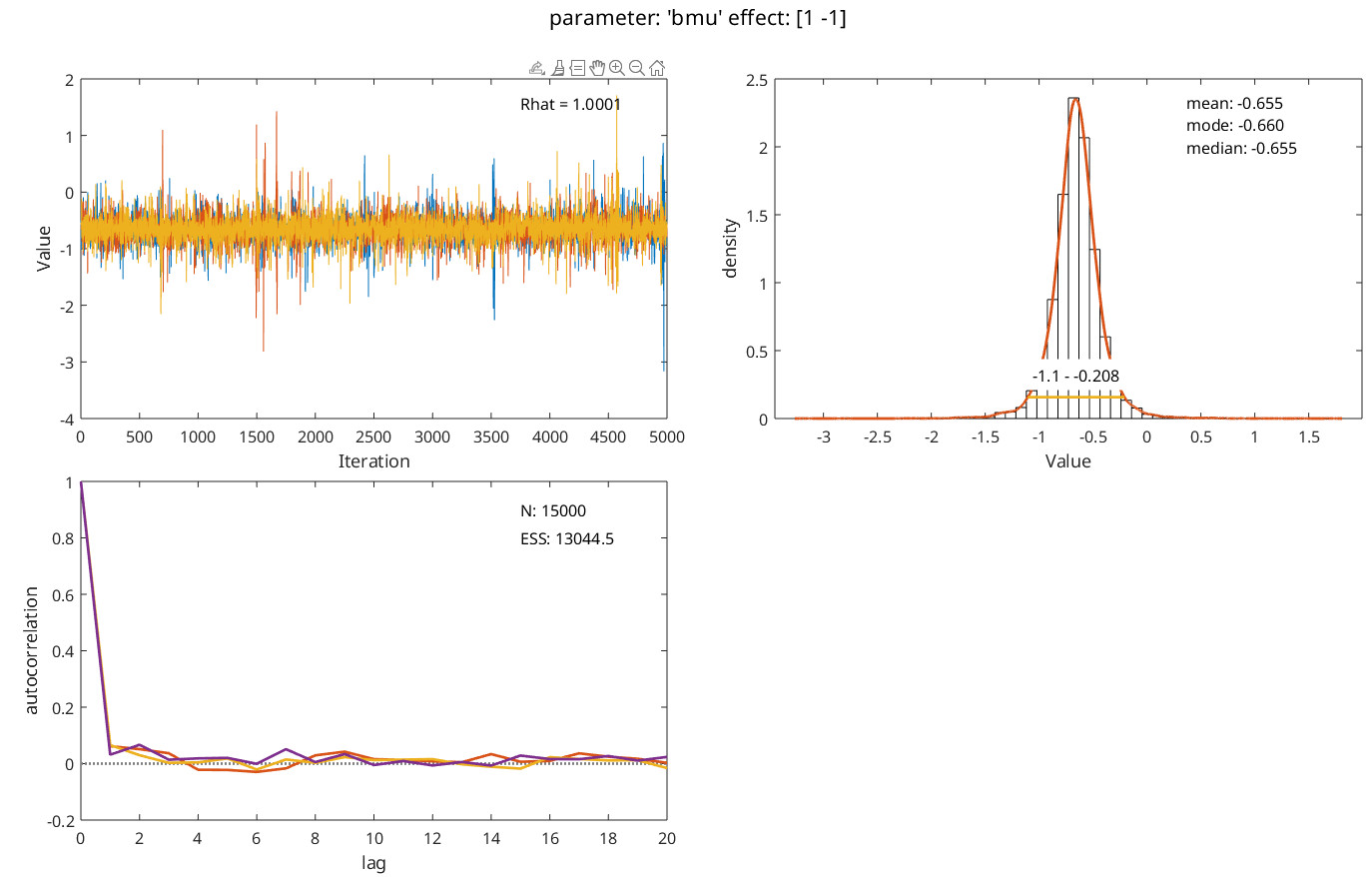
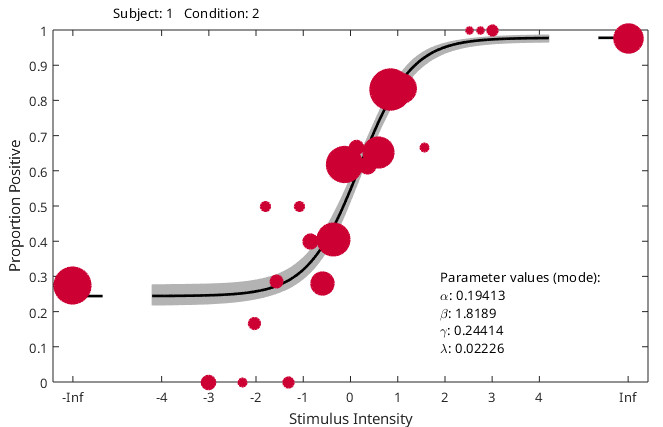
Overall, for your circumstances (s far as we understand them) we recommend something like the following code. It generates some data with a different generating value for slope between conditions (and observers), random false alarm rates that differ between conditions and observers and lapse rates that differ between observers, but not between conditions for any observer. Data are then analyzed with slopes reparameterized into a mean-slope (across conditions) parameter and a difference-between-slopes parameter. Guess rates are based on all data (but the model ‘knows’ that on foil trials no stimulus was present because stimulus intensity there is given as -Inf). Code also demonstrates how to use priors with different means for the mean (across observers) of the location (‘threshold’) parameter. Code then draws violin plots for the hyper parameters. Note that x-axis for the plot of the slope hyperparameters is labeled ‘effect’ (not 'condition'). This is because it does not plot the two slopes. Rather it plots the posterior for the hyperparameter corresponding to the mean of the slopes across conditions (effect 1) and the posterior for the hyperparameters corresponding to the difference between the slopes (effect 2). It then plots the posterior for the latter in some more detail with some diagnostics. It then shows individual fits for all observers and conditions (cycle through using <enter>)
Hope all of that made sense. If not, let me know.
Groeten,
Nick
Glad to hear you find Palamedes useful and gives you good fits.
Currently, the PFHB routines do not allow comparing groups of observers. You can compare individual observers against other individual observers but that’s it. You can of course run two separate analyses, one for each group, then compare posteriors or summary statistics for the hyperparameters (or observer-level parameters) between the two groups.
Palamedes does not directly allow fixing guess rates at different values for different subjects and/or sessions. But there is a work-around to accomplish that. I’ll explain the work-around below. However, before I do that I’m going to try to talk you out of taking that approach. Here goes. Trials at intensities other than ‘-Inf’ contain information on the false alarm rate also. Consider this hypothetical, but not implausible, scenario: Let’s say an observer responds ‘yes’ on a proportion of 0.4 of foil (‘-Inf’) trials. Let’s also say that on the trials where the lowest intensity (but greater than -Inf) is used, the observer responds ‘yes’ on a proportion of, say, 0.3 of trials. The latter of course would suggest that 0.4 might be an overestimate of the false alarm rate. What should you use for the probability of the false alarm rate? Is it better to fix it at .4 or to let the model do its thing and take into account all the information? Note that you can include the ‘-Inf’ trials in the overall analysis (just use the value ‘-Inf’ as an intensity value, I demonstrate this in the code below). If the data at the trials where intensity was not ‘-Inf’ give little information about the value of the false alarm rate, then you’ll find that Palamedes’ estimate for the guess rate appropriately will be close to the observed proportion ‘yes’ at ‘-Inf’ trials (assuming the prior is not too informative). But if there is information at the other trials (as in the above hypothetical example), the model will, again appropriately, adjust its estimate accordingly. Another way to think about it is that using a fixed value for a parameter in a Bayesian analysis is equivalent to supplying an infinitely narrow prior (or point prior). In other words, you would be pretending that there is no uncertainty regarding the value of the false alarm rate. But there is uncertainty, and so you would be misinforming the model. And if you misinform your model, your results suffer.
Here is the workaround for fixing the false alarms rate at different values for different conditions. Code given is for a single observer analysis. The strategy is to specify different priors in the different conditions and make those priors very tight. In the example code, the gues rate for condition 1 would (effectively) be fixed at 0.1, for condition 2 at .2. You can generalize to a multiple observer analysis. You would have to create a very tight prior on gmu parameter at the to-be-fixed value and create a prior on gkappa that only contains very high values. That would force all guess rates to be near the targeted value. Again, we recommend against all of this.
Code: Select all
pfhb = PAL_PFHB_fitModel(data,'g',[1 0; 0 1],'prior','g','beta',[.1 100000000; .2 100000000],'PF','gumbel');
In order to test whether slope parameters differ between conditions, the recommended strategy is to reparameterize the two slopes into a mean (across conditions) slope parameter and a difference-between-slopes parameter. The test criterion could then be to determine whether 0 is a credible value for the difference parameter.
Overall, for your circumstances (s far as we understand them) we recommend something like the following code. It generates some data with a different generating value for slope between conditions (and observers), random false alarm rates that differ between conditions and observers and lapse rates that differ between observers, but not between conditions for any observer. Data are then analyzed with slopes reparameterized into a mean-slope (across conditions) parameter and a difference-between-slopes parameter. Guess rates are based on all data (but the model ‘knows’ that on foil trials no stimulus was present because stimulus intensity there is given as -Inf). Code also demonstrates how to use priors with different means for the mean (across observers) of the location (‘threshold’) parameter. Code then draws violin plots for the hyper parameters. Note that x-axis for the plot of the slope hyperparameters is labeled ‘effect’ (not 'condition'). This is because it does not plot the two slopes. Rather it plots the posterior for the hyperparameter corresponding to the mean of the slopes across conditions (effect 1) and the posterior for the hyperparameters corresponding to the difference between the slopes (effect 2). It then plots the posterior for the latter in some more detail with some diagnostics. It then shows individual fits for all observers and conditions (cycle through using <enter>)
Code: Select all
Ncond = 2;
Nsubj = 6;
Ntrials = 500;
PF = @PAL_Logistic;
%Generate some data using adaptive psi-method (type help PAL_AMPM_setupPM
%for more information)
grain = 26;
%Define parameter ranges to be included in posterior
priorAlphaRange = linspace(-2, 2,grain);
priorBetaRange = linspace(-1,1,grain); %Use log10 transformed values of beta (slope) parameter in PF
priorGammaRange = 0:.05:.4; %Value shown here is inconsequential: guess rate will be constrained to be equal to lapse rate
priorLambdaRange = 0:.01:.1;
stimRange = [-Inf linspace(-3,3,26) Inf];
[a b g l] = ndgrid(priorAlphaRange,priorBetaRange,priorGammaRange,priorLambdaRange);
%generating parameters
for cond = 1:Ncond
a_gen(cond,1:Nsubj) = .25*randn(1)+randn(1,Nsubj)*.5;
b_gen(cond,1:Nsubj) = -.25 + (cond-1)*.5 + randn(1,Nsubj)*.25;
g_gen(cond,1:Nsubj) = .25 + randn(1,Nsubj)*.1;
end
l_gen = repmat([.01 .02 .03 .07 .01 .04],[Ncond,1]); %different lapse rate for each subjects
g_gen(g_gen < 0) = 0;
data.x = [];
data.s = [];
data.c = [];
data.y = [];
data.n = [];
for c = 1:Ncond
for s = 1:Nsubj
c
s
paramsGen = [a_gen(c,s), 10.^b_gen(c,s), g_gen(c,s), l_gen(c,s)]; %parameter values [alpha, beta, gamma, lambda] (or [threshold, slope, guess, lapse]) used to simulate observer
%Initialize PM structure
PM = PAL_AMPM_setupPM('priorAlphaRange',priorAlphaRange,...
'priorBetaRange',priorBetaRange,...
'priorGammaRange',priorGammaRange,...
'priorLambdaRange',priorLambdaRange,...
'numtrials',Ntrials,...
'PF' , PF,...
'stimRange',stimRange,...
'marginalize',[3 4],...
'gammaeqlambda',false);
%trial loop
while PM.stop ~= 1
response = rand(1) < PF(paramsGen, PM.xCurrent); %simulate observer
%update PM based on response
PM = PAL_AMPM_updatePM(PM,response);
end
[xG yG nG] = PAL_PFML_GroupTrialsbyX(PM.x(1:end-1),PM.response,ones(size(PM.response)));
data.x = [data.x xG];
data.y = [data.y yG];
data.n = [data.n nG];
data.c = [data.c c*ones(size(xG))];
data.s = [data.s s*ones(size(xG))];
end
end
[pfhb] = PAL_PFHB_fitModel(data,'b',[.5 .5; 1 -1],'g','unconstrained','prior','gmu','beta',[.2 10; .2 10],'prior','amu','norm',[0 10; 1 10]);
PAL_PFHB_drawViolins(pfhb)
PAL_PFHB_inspectParam(pfhb,'bmu','effect',2)
PAL_PFHB_inspectFit(pfhb,'all')


Hope all of that made sense. If not, let me know.
Groeten,
Nick
Nick Prins, Administrator
Re: Fixing false alarm rate per condition/subject
Hi Nick,
Thanks for your helpful reply!
I successfully compared the slopes at the two frequencies for the two groups separately. The fits with guess rate (and lapse rate) unconstrained look good, so you convinced me to use this instead of the value at -Inf .
Did I understand correctly from your post that it is not possible in PAL_PFHB_fitModel to compare the two groups and frequencies and their interaction as in the 2 x 2 factorial design example on https://www.palamedestoolbox.org/modelmatrix.html?
Met vriendelijke groet,
Gerard
Thanks for your helpful reply!
I successfully compared the slopes at the two frequencies for the two groups separately. The fits with guess rate (and lapse rate) unconstrained look good, so you convinced me to use this instead of the value at -Inf .
Did I understand correctly from your post that it is not possible in PAL_PFHB_fitModel to compare the two groups and frequencies and their interaction as in the 2 x 2 factorial design example on https://www.palamedestoolbox.org/modelmatrix.html?
Met vriendelijke groet,
Gerard
- Nick Prins
- Site Admin
- Posts: 28
- Joined: Sun Feb 13, 2022 8:55 pm
Re: Fixing false alarm rate per condition/subject
Glad to hear I was helpful. Correct, Palamedes currently does not support including between-subject factors in a factorial (or other) design. Effects across multiple factors and their interactions can be defined but only across within-subject conditions.
Nick Prins, Administrator